বিস্তার পরিমাপ

বিস্তার পরিমাপ (Measures of Dispersion) হলো উপাত্তের ভিন্নতা বা বৈচিত্র্য নির্ধারণের পদ্ধতি। এটি ডেটাসেটের কেন্দ্রীয় প্রবণতা থেকে উপাত্ত কতটা ছড়ানো বা একত্রিত হয়েছে, তা পরিমাপ করতে সাহায্য করে। বিস্তার পরিমাপ আমাদের ডেটার সঠিক বৈচিত্র্য এবং স্থিরতার পরিমাণ বুঝতে সহায়তা করে।

বিস্তার পরিমাপের প্রকারভেদ

বিস্তার পরিমাপের বিভিন্ন প্রকারভেদ নিম্নরূপ:

পরিসর (Range)

সংজ্ঞা:
ডেটাসেটের সর্বাধিক মান এবং সর্বনিম্ন মানের পার্থক্যকে পরিসর বলা হয়।

সূত্র:

উদাহরণ:
ডেটাসেট: ৫, ৭, ১০, ১৫, ২০
পরিসর = ২০ - ৫ = ১৫

বৈশিষ্ট্য:

• এটি সরাসরি ডেটার বৈচিত্র্য দেখায়।
• চরম মান বা outlier দ্বারা খুব প্রভাবিত হয়।

চতুর্থাংশ বিস্তার (Quartile Deviation)

সংজ্ঞা:
ডেটাসেটের প্রথম চতুর্থাংশ (Q1) এবং তৃতীয় চতুর্থাংশ (Q3) এর মধ্যে পার্থক্যকে চতুর্থাংশ বিস্তার বলা হয়।

সূত্র:

চতুর্থাংশ বিস্তার = Q3 - Q1

উদাহরণ:
ডেটাসেট: ১, ৩, ৫, ৭, ৯, ১১, ১৩
Q1 = ৩, Q3 = ১১
চতুর্থাংশ বিস্তার = ১১ - ৩ = ৮

বৈশিষ্ট্য:

• চরম মান দ্বারা কম প্রভাবিত হয়।
• ডেটার মধ্যবর্তী বৈচিত্র্য বোঝাতে কার্যকর।

গড় বিচ্যুতি (Mean Deviation)

সংজ্ঞা:
গড় থেকে ডেটাসেটের প্রতিটি মানের গড় বিচ্যুতি নির্ণয় করা হয়।

সূত্র:

উদাহরণ:
ডেটাসেট: ২, ৪, ৬, ৮
গড় = (২ + ৪ + ৬ + ৮) / ৪ = ৫
গড় বিচ্যুতি = [(|২-৫|) + (|৪-৫|) + (|৬-৫|) + (|৮-৫|)] / ৪ = ২

বৈশিষ্ট্য:

• এটি ডেটার সাধারণ বৈচিত্র্য নির্দেশ করে।
• সহজ এবং কার্যকর।

বর্গমূল বিচ্যুতি বা মানক বিচ্যুতি (Standard Deviation)

সংজ্ঞা:
ডেটাসেটের প্রতিটি মান থেকে গড়ের বর্গমূল বিচ্যুতি নির্ণয় করে মানক বিচ্যুতি নির্ধারণ করা হয়।

সূত্র:

উদাহরণ:
ডেটাসেট: ২, ৪, ৬
গড় = (২ + ৪ + ৬) / ৩ = ৪

বৈশিষ্ট্য:

• এটি ডেটাসেটের বৈচিত্র্য পরিমাপের সবচেয়ে নির্ভরযোগ্য পদ্ধতি।
• এটি গাণিতিক এবং পরিসংখ্যান বিশ্লেষণে বেশি ব্যবহৃত হয়।

বিস্তার পরিমাপের প্রয়োজনীয়তা

1. উপাত্তের বৈচিত্র্য বুঝতে:
   এটি ডেটাসেটের বিভিন্নতা ও স্থিরতা নির্ধারণে সহায়ক।
2. কেন্দ্রীয় প্রবণতার সঠিকতা যাচাই করতে:
   বিস্তার পরিমাপ কেন্দ্রীয় প্রবণতা পরিমাপগুলোর (যেমন গড়) বিশ্বাসযোগ্যতা মূল্যায়ন করে।
3. তুলনা করতে:
   ভিন্ন ভিন্ন ডেটাসেটের বৈচিত্র্যের তুলনা করার জন্য।

সারসংক্ষেপ

বিস্তার পরিমাপ ডেটাসেটের বৈচিত্র্য ও বিচ্যুতি বুঝতে একটি গুরুত্বপূর্ণ পদ্ধতি। পরিসর, চতুর্থাংশ বিস্তার, গড় বিচ্যুতি, এবং মানক বিচ্যুতি বিভিন্ন ধরনের উপাত্তের বৈচিত্র্য বিশ্লেষণে ব্যবহৃত হয়। ডেটার প্রকৃতি অনুযায়ী সঠিক বিস্তার পরিমাপ বেছে নেওয়া দরকার।

বিস্তার (Range)

বিস্তার হলো একটি ডেটাসেটের সর্বোচ্চ এবং সর্বনিম্ন মানের মধ্যে পার্থক্য। এটি ডেটাসেটের বিভিন্নতার একটি সহজ পরিমাপ এবং ডেটার বিতরণের প্রাথমিক ধারণা দেয়।

বিস্তার নির্ণয়ের সূত্র:

উদাহরণ:
ডেটাসেট: 5, 10, 15, 20, 25
বিস্তার: 25 - 5 = 20

বিস্তার পরিমাপ (Measure of Dispersion)

বিস্তার পরিমাপ ডেটাসেটের মানগুলোর ছড়িয়ে পড়ার মাত্রা বা ডেটা কতটা ছড়ানো তা বোঝায়। এটি মূলত ডেটাসেটের বৈচিত্র্য এবং স্থিতি নির্ধারণে ব্যবহৃত হয়।

ডেটা বিশ্লেষণে বিস্তার পরিমাপ অত্যন্ত গুরুত্বপূর্ণ, কারণ এটি ডেটার গুণমান এবং স্থিতিশীলতার ধারণা দেয়।

বিস্তার পরিমাপের প্রকারভেদ (Types of Measures of Dispersion)

বিস্তার পরিমাপ প্রধানত দুটি ভাগে বিভক্ত:

১. সহজ বিস্তার পরিমাপ (Absolute Measure of Dispersion)

এটি ডেটাসেটের বাস্তব পরিমাপ ব্যবহার করে বিস্তার নির্ণয় করে। সাধারণত এই ধরনের পরিমাপ ডেটাসেটের বিভিন্নতার সঠিক মান প্রকাশ করে। এর প্রধান প্রকারগুলো হলো:

ক. বিস্তার (Range):
সর্বোচ্চ এবং সর্বনিম্ন মানের মধ্যে পার্থক্য।
Range = Maximum Value -Minimum Value

খ. আন্তঃচতুর্থাংশ বিস্তার (Interquartile Range):
ডেটাসেটের ৭৫তম শতাংশক (Q3) এবং ২৫তম শতাংশক (Q1)-এর মধ্যে পার্থক্য।
IQR = Q3 - Q1

গ. চতুর্ভাগীয় বিচ্যুতি (Quartile Deviation):

ঘ. গড় বিচ্যুতি (Mean Deviation):
ডেটাসেটের প্রতিটি মানের গড় থেকে বিচ্যুতির গড়।

২. আপেক্ষিক বিস্তার পরিমাপ (Relative Measure of Dispersion)

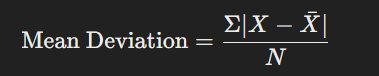
আপেক্ষিক বিস্তার পরিমাপ ডেটার বিভিন্নতার তুলনামূলক মাত্রা নির্দেশ করে এবং এটি সাধারণত শতাংশে প্রকাশিত হয়। এর প্রধান প্রকারগুলো হলো:

ক. আপেক্ষিক গড় বিচ্যুতি (Relative Mean Deviation):
গড় বিচ্যুতিকে গড়ের সাথে তুলনা করে নির্ণয় করা হয়।

খ. আপেক্ষিক চতুর্ভাগীয় বিচ্যুতি (Relative Quartile Deviation):

গ. আপেক্ষিক মান বিচ্যুতি (Relative Standard Deviation):
ডেটাসেটের মান বিচ্যুতিকে গড় বা মধ্যকের সাথে তুলনা করা হয়।

বিস্তার পরিমাপের গুরুত্ব

১. ডেটাসেটের বৈচিত্র্য এবং স্থিতি নির্ধারণে সহায়তা করে।
২. বিভিন্ন ডেটাসেটের তুলনা করতে ব্যবহৃত হয়।
৩. গাণিতিক বিশ্লেষণে ডেটাসেটের স্থায়িত্ব যাচাই করা যায়।
৪. ডেটার চরম মান শনাক্তে সহায়তা করে।

সারসংক্ষেপ

বিস্তার এবং বিস্তার পরিমাপ ডেটাসেটের বৈচিত্র্য বোঝার জন্য গুরুত্বপূর্ণ। এটি ডেটার বিস্তৃতি এবং বিভাজন সম্পর্কে একটি পরিষ্কার ধারণা দেয়। বিভিন্ন ধরনের বিস্তার পরিমাপ বিভিন্ন পরিস্থিতিতে ব্যবহৃত হয়, যা ডেটা বিশ্লেষণে অত্যন্ত কার্যকর।

অনপেক্ষ বা পরম বিস্তার পরিমাপের প্রকারভেদ (Types of Absolute Measures of Dispersion)

অনপেক্ষ বা পরম বিস্তার পরিমাপ (Absolute Measures of Dispersion) হলো পরিসংখ্যানের একটি পদ্ধতি, যার মাধ্যমে ডেটাসেটের মানগুলোর মধ্যে বৈচিত্র্য বা বিচ্ছুরণ পরিমাপ করা হয়। এই পরিমাপগুলো সরাসরি মূল ডেটাসেটের একক বা মান ব্যবহার করে ডেটার মধ্যে পরিবর্তনশীলতার মাত্রা নির্ধারণ করে। এর প্রধান প্রকারভেদগুলো হলো:

১. পরিসর (Range)

সংজ্ঞা:
ডেটাসেটের সর্বোচ্চ এবং সর্বনিম্ন মানের মধ্যকার পার্থক্য হলো পরিসর। এটি ডেটার বৈচিত্র্যের একটি সরলতম পরিমাপ।

সূত্র:
Range= সর্বোচ্চ মান - সর্বনিম্ন মান

উদাহরণ:
ডেটাসেট: 5, 8, 12, 20
পরিসর: 20 - 5 = 15

গুণাবলি:

• সরল এবং দ্রুত গণনা করা যায়।
• তবে এটি কেবল চূড়ান্ত মানগুলোর উপর নির্ভরশীল, মধ্যবর্তী মান বিবেচনা করে না।

২. আন্তর্চতুর্থাংশ বিস্তৃতি (Interquartile Range)

সংজ্ঞা:
ডেটাসেটের প্রথম চতুর্থাংশ (Q1) এবং তৃতীয় চতুর্থাংশ (Q3)-এর মধ্যকার পার্থক্য হলো আন্তর্চতুর্থাংশ বিস্তৃতি। এটি মধ্যবর্তী ৫০% ডেটার বৈচিত্র্য পরিমাপ করে।

সূত্র:
IQR} = Q3 - Q1

উদাহরণ:
ডেটাসেট: 4, 8, 10, 12, 16, 20, 24
Q1 = 8 , Q3 = 20
IQR: 20 - 8 = 12

গুণাবলি:

• মধ্যবর্তী ডেটার ওপর ভিত্তি করে বৈচিত্র্য নির্ধারণ করে।
• চূড়ান্ত মানগুলোর প্রভাব কম থাকে।

৩. গড় বিচ্যুতি (Mean Deviation)

সংজ্ঞা:
ডেটাসেটের প্রতিটি মান এবং গড়ের মধ্যকার পার্থক্যের গড় হলো গড় বিচ্যুতি।

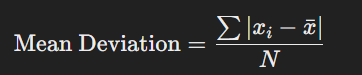
সূত্র:

যেখানে:

উদাহরণ:
ডেটাসেট: 5, 7, 9

Mean Deviation:

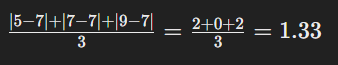
গুণাবলি:

• গড়ের চারপাশের ডেটার বিচ্যুতি পরিমাপ করে।
• ডেটার সমানভাবে বিতরণ বোঝায়।

৪. মানক বিচ্যুতি (Standard Deviation)

সংজ্ঞা:
ডেটাসেটের প্রতিটি মান এবং গড়ের মধ্যকার বিচ্যুতি (Deviation)-এর বর্গের গড়ের বর্গমূল হলো মানক বিচ্যুতি। এটি ডেটার বৈচিত্র্য পরিমাপের সবচেয়ে গুরুত্বপূর্ণ এবং ব্যাপকভাবে ব্যবহৃত পদ্ধতি।

সূত্র:

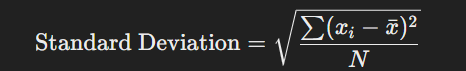
উদাহরণ:
ডেটাসেট: 6, 8, 10

Variance:

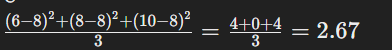
Standard Deviation:

গুণাবলি:

• ডেটার বিচ্যুতি বিশ্লেষণে সবচেয়ে নির্ভুল।
• জটিল সমস্যাগুলোর জন্য কার্যকর।

৫. বৈচিত্র্যের যোগফল (Variance)

সংজ্ঞা:
ডেটাসেটের প্রতিটি মান এবং গড়ের মধ্যকার বিচ্যুতির বর্গের গড় হলো বৈচিত্র্যের যোগফল।

সূত্র:

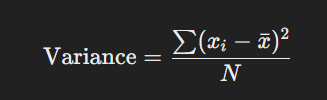
গুণাবলি:

• এটি মানক বিচ্যুতির পূর্বধাপ।
• গড় থেকে ডেটার বিচ্যুতির একটি ধারণা প্রদান করে।

সারসংক্ষেপ

অনপেক্ষ বা পরম বিস্তার পরিমাপের বিভিন্ন পদ্ধতি ডেটাসেটের ভিন্ন ভিন্ন বৈচিত্র্য বিশ্লেষণে কার্যকর। সরল পরিসর থেকে শুরু করে মানক বিচ্যুতি পর্যন্ত প্রতিটি পদ্ধতি নির্দিষ্ট প্রেক্ষাপটে ডেটার বৈচিত্র্য বা বিচ্যুতি বিশ্লেষণে সহায়ক।

বিস্তার পরিমাপের গুরুত্ব ও প্রয়োজনীয়তা

বিস্তার পরিমাপ উপাত্তের বৈচিত্র্য বা ছড়ানোর মাত্রা নির্ণয় করে। এটি পরিসংখ্যান বিশ্লেষণের একটি গুরুত্বপূর্ণ অংশ, যা কেন্দ্রীয় প্রবণতা পরিমাপগুলোর সাথে মিলিত হয়ে ডেটাসেট সম্পর্কে আরও গভীর ধারণা প্রদান করে। নিচে বিস্তার পরিমাপের গুরুত্ব ও প্রয়োজনীয়তা নিয়ে আলোচনা করা হলো:

গুরুত্ব

১. উপাত্তের বৈচিত্র্য নির্ধারণ

বিস্তার পরিমাপ একটি ডেটাসেটে উপাত্তের পরিসরের পরিমাণ বা ছড়ানোর মাত্রা প্রকাশ করে। এটি বোঝায় যে উপাত্তগুলি কতটা কাছাকাছি বা দূরে অবস্থিত।

উদাহরণ:
যদি দুটি ক্লাসের পরীক্ষার ফলাফল বিশ্লেষণ করা হয় এবং দেখা যায় একটি ক্লাসের পরিসর ১০ এবং অন্যটির ৩০, তবে বোঝা যায় দ্বিতীয় ক্লাসে বৈচিত্র্য বেশি।

২. কেন্দ্রীয় প্রবণতার সঠিকতা যাচাই

বিস্তার পরিমাপ কেন্দ্রীয় প্রবণতা পরিমাপগুলোর (যেমন গড়, মধ্যক) নির্ভরযোগ্যতা যাচাই করতে সাহায্য করে।

• একটি ছোট পরিসর নির্দেশ করে গড়টি ডেটার প্রকৃত অবস্থার প্রতিনিধিত্ব করছে।
• বড় পরিসর নির্দেশ করে গড়টি প্রকৃত অবস্থার থেকে বিচ্যুত হতে পারে।

৩. সিদ্ধান্ত গ্রহণে সহায়ক

বিস্তার পরিমাপ বিভিন্ন পরিস্থিতিতে কার্যকর সিদ্ধান্ত গ্রহণে সাহায্য করে। এটি ব্যবসা, শিক্ষা, গবেষণা এবং আর্থিক ব্যবস্থাপনায় গুরুত্বপূর্ণ ভূমিকা পালন করে।

উদাহরণ:
দুটি স্টকের মধ্যে যেটির মূল্য বেশি পরিবর্তনশীল (বেশি বিস্তার), সেটি বিনিয়োগের জন্য ঝুঁকিপূর্ণ হতে পারে।

৪. তুলনা করার সুবিধা

বিভিন্ন ডেটাসেটের বিস্তার নির্ধারণ করে তাদের মধ্যে বৈচিত্র্যের তুলনা করা সম্ভব।

উদাহরণ:
দুটি স্কুলের পরীক্ষার ফলাফলের বিস্তার পরিমাপ করে বোঝা যায় কোন স্কুলে শিক্ষার্থীদের মধ্যে ফলাফলের বৈচিত্র্য বেশি।

৫. ডেটার স্থিরতা বা স্থায়িত্ব নির্ধারণ

বিস্তার পরিমাপের মাধ্যমে ডেটা কতটা স্থির বা পরিবর্তনশীল তা বোঝা যায়। কম বিস্তার স্থায়িত্ব নির্দেশ করে এবং বেশি বিস্তার পরিবর্তনশীলতা নির্দেশ করে।

প্রয়োজনীয়তা

১. ডেটার বৈচিত্র্য বুঝতে

যে কোনো গবেষণা বা বিশ্লেষণের জন্য ডেটাসেটের বৈচিত্র্য জানা অত্যন্ত গুরুত্বপূর্ণ। এটি ডেটা কতটা ছড়ানো তা বোঝায়।

২. গড় ও মধ্যকের কার্যকারিতা নিশ্চিত করতে

গড় বা মধ্যক প্রায়ই চরম মান দ্বারা প্রভাবিত হয়। বিস্তার পরিমাপ এটি সঠিকভাবে বুঝতে সাহায্য করে।

৩. গবেষণায় উপাত্তের সামঞ্জস্যতা যাচাই

গবেষণায় ডেটাসেট কতটা সামঞ্জস্যপূর্ণ তা বিশ্লেষণের জন্য বিস্তার পরিমাপ প্রয়োজন।

উদাহরণ:
একটি ওষুধের কার্যকারিতা পরীক্ষা করতে বিস্তার পরিমাপ ব্যবহার করা হয়। কম বিস্তার মানে ওষুধটির কার্যকারিতা নির্ভরযোগ্য।

৪. পূর্বাভাস তৈরি করা

ডেটার বৈচিত্র্যের ভিত্তিতে ভবিষ্যৎ প্রবণতা অনুমান করা সহজ হয়।

৫. ঝুঁকি বিশ্লেষণ

বিস্তার পরিমাপ ঝুঁকি বিশ্লেষণে গুরুত্বপূর্ণ। এটি জানায় ডেটা কতটা পরিবর্তনশীল এবং সংশ্লিষ্ট ঝুঁকি কতটা বেশি।

সারসংক্ষেপ

বিস্তার পরিমাপ শুধু উপাত্তের বৈচিত্র্য নির্ণয় নয়, বরং বিভিন্ন সিদ্ধান্ত গ্রহণ, গবেষণার নির্ভুলতা নিশ্চিত করা, এবং ভবিষ্যৎ প্রবণতা নির্ধারণে গুরুত্বপূর্ণ ভূমিকা পালন করে। এটি উপাত্ত বিশ্লেষণের একটি অপরিহার্য অংশ।

একটি আদর্শ বিস্তারের গুণাবলি

একটি আদর্শ বিস্তার (Measure of Dispersion) ডেটাসেটের বৈচিত্র্য এবং পরিবর্তনশীলতা সঠিকভাবে বোঝাতে কিছু নির্দিষ্ট গুণাবলির অধিকারী হওয়া উচিত। সেগুলো নিম্নরূপ:

১. সহজতা

• আদর্শ বিস্তার গণনা করা সহজ হওয়া উচিত, যাতে এটি বিভিন্ন প্রয়োগক্ষেত্রে ব্যবহার করা যায়।
• যেমন: গড় বিচ্যুতি (Mean Deviation) এবং মধ্যম মান বিচ্যুতি (Median Deviation) সহজেই গণনা করা যায়।

২. স্পষ্টতা

• এটি স্পষ্টভাবে ডেটাসেটের ভিন্নতা বা পরিবর্তনশীলতার প্রকৃতি নির্দেশ করতে সক্ষম হতে হবে।
• যেমন: স্ট্যান্ডার্ড ডেভিয়েশন একটি সাধারণ ও স্পষ্ট পদ্ধতি।

৩. সংবেদনশীলতা (Sensitivity)

• আদর্শ বিস্তার ডেটাসেটের সমস্ত মানের প্রতি সংবেদনশীল হওয়া উচিত।
• উদাহরণ: ভ্যারিয়েন্স এবং স্ট্যান্ডার্ড ডেভিয়েশন ডেটাসেটের প্রতিটি মানকে বিবেচনায় নেয়।

৪. চরম মানের প্রভাব প্রতিরোধ

• একটি আদর্শ বিস্তার চরম মান বা অস্বাভাবিক মান দ্বারা খুব বেশি প্রভাবিত হওয়া উচিত নয়।
• উদাহরণ: ইন্টার-কোয়ার্টাইল রেঞ্জ (IQR) চরম মানের প্রভাব থেকে সুরক্ষিত।

৫. এককতা (Unit Consistency)

• বিস্তারের পরিমাপের একক ডেটার এককের সাথে সামঞ্জস্যপূর্ণ হওয়া উচিত।
• উদাহরণ: স্ট্যান্ডার্ড ডেভিয়েশন এবং গড় বিচ্যুতি ডেটার একক ধরে রাখে।

৬. বৈচিত্র্যপূর্ণ পরিস্থিতিতে প্রযোজ্যতা

• আদর্শ বিস্তার এমন একটি পদ্ধতি হওয়া উচিত যা বিভিন্ন ধরণের ডেটাসেটে প্রযোজ্য।
• উদাহরণ: ভ্যারিয়েন্স এবং স্ট্যান্ডার্ড ডেভিয়েশন প্রায় সব ধরনের ডেটাসেটে ব্যবহার করা যায়।

৭. পরিসংখ্যান বিশ্লেষণে সহায়ক

• এটি এমন তথ্য প্রদান করতে হবে যা পরিসংখ্যানগত বিশ্লেষণে উপকারী।
• উদাহরণ: স্ট্যান্ডার্ড ডেভিয়েশন ডেটাসেটের প্রায় সব ধরনের বিচ্যুতি বিশ্লেষণে ব্যবহৃত হয়।

৮. সহজ তুলনা করার উপযোগিতা

• বিভিন্ন ডেটাসেটের বিস্তারের তুলনা করা সহজ হওয়া উচিত।
• উদাহরণ: কোএফিসিয়েন্ট অব ভ্যারিয়েশন (Coefficient of Variation) তুলনা করার জন্য কার্যকর।

সারসংক্ষেপ

একটি আদর্শ বিস্তার সহজ, স্পষ্ট, সংবেদনশীল, এবং চরম মানের প্রভাব থেকে মুক্ত হওয়া উচিত। এটি পরিসংখ্যান বিশ্লেষণ এবং তুলনার জন্য কার্যকর হওয়া প্রয়োজন। ডেটার প্রকৃতি অনুযায়ী সঠিক বিস্তার পরিমাপ নির্বাচন গুরুত্বপূর্ণ।

বিস্তার পরিমাপসমূহের তুলনামূলক আলোচনা

ডেটাসেটের বৈচিত্র্য এবং ছড়িয়ে পড়া সম্পর্কে ধারণা পেতে বিস্তার পরিমাপ গুরুত্বপূর্ণ। প্রতিটি পরিমাপের নির্দিষ্ট বৈশিষ্ট্য এবং সুবিধা রয়েছে। নিচে বিস্তার পরিমাপের বিভিন্ন পদ্ধতির তুলনামূলক আলোচনা উপস্থাপন করা হলো:

১. বিস্তার (Range)

বৈশিষ্ট্য:

• সহজে গণনা করা যায়।
• সর্বোচ্চ এবং সর্বনিম্ন মানের মধ্যে পার্থক্য নির্ণয় করে।

সুবিধা:

• ডেটাসেটের বিস্তৃতি সম্পর্কে সরাসরি ধারণা দেয়।
• কম সময়ে এবং সহজে ব্যবহৃত হয়।

অসুবিধা:

• চরম মান বা বহিরাগত মান (Outliers) এর প্রভাব খুব বেশি।
• ডেটাসেটের মধ্যবর্তী মানগুলোর ছড়িয়ে পড়ার তথ্য দেয় না।

২. আন্তঃচতুর্থাংশ বিস্তার (Interquartile Range - IQR)

বৈশিষ্ট্য:

• ডেটাসেটের ২৫তম শতাংশক (Q1) এবং ৭৫তম শতাংশক (Q3)-এর মধ্যে পার্থক্য নির্ণয় করে।

সুবিধা:

• চরম মান বা বহিরাগত মান দ্বারা প্রভাবিত হয় না।
• ডেটাসেটের মধ্যবর্তী অংশের বৈচিত্র্য ভালোভাবে প্রকাশ করে।

অসুবিধা:

• শুধুমাত্র ডেটার মধ্যবর্তী ৫০% অংশ বিবেচনা করে; সম্পূর্ণ ডেটাসেটের বৈচিত্র্যের ধারণা দেয় না।

৩. গড় বিচ্যুতি (Mean Deviation)

বৈশিষ্ট্য:

• প্রতিটি মান এবং গড়ের (বা মধ্যক) মধ্যে পার্থক্যের গড় নির্ণয় করে।

সুবিধা:

• ডেটাসেটের সমস্ত মানের বৈচিত্র্যের ভালো পরিমাপ দেয়।
• তুলনামূলকভাবে চরম মানের প্রভাব কম।

অসুবিধা:

• গণনা অপেক্ষাকৃত বেশি সময়সাপেক্ষ।
• গড়ের পরিবর্তে মধ্যকের উপর ভিত্তি করে হিসাব করলে কম প্রভাবিত হয়।

৪. চতুর্ভাগীয় বিচ্যুতি (Quartile Deviation)

বৈশিষ্ট্য:

• মধ্যবর্তী ৫০% ডেটার বৈচিত্র্যের একটি সহজ পরিমাপ।

সুবিধা:

• বহিরাগত মান দ্বারা প্রভাবিত হয় না।
• ডেটাসেটের মূল অংশের বৈচিত্র্য সঠিকভাবে নির্দেশ করে।

অসুবিধা:

• ডেটাসেটের সম্পূর্ণ বৈচিত্র্য প্রকাশ করে না।

৫. মান বিচ্যুতি (Standard Deviation)

বৈশিষ্ট্য:

• ডেটাসেটের প্রতিটি মানের গড় থেকে বিচ্যুতির বর্গমূল নির্ণয় করে।

সুবিধা:

• ডেটাসেটের পুরো বৈচিত্র্য সম্পর্কে নির্ভুল ধারণা দেয়।
• বিভিন্ন ডেটাসেটের তুলনা করতে কার্যকর।

অসুবিধা:

• চরম মান দ্বারা প্রভাবিত হয়।
• গণনা তুলনামূলকভাবে জটিল।

তুলনামূলক চিত্র

সারসংক্ষেপ

বিস্তার পরিমাপ নির্বাচন করার সময় ডেটাসেটের প্রকৃতি এবং প্রয়োজনীয় বিশ্লেষণের উপর নির্ভর করতে হয়।

• বিস্তার (Range) সহজ বিশ্লেষণে কার্যকর।
• আন্তঃচতুর্থাংশ বিস্তার (IQR) বহিরাগত মান থাকা ডেটাসেটের জন্য ভালো।
• মান বিচ্যুতি (Standard Deviation) জটিল এবং নির্ভুল বিশ্লেষণের জন্য আদর্শ।
  বিভিন্ন পরিস্থিতিতে বিভিন্ন বিস্তার পরিমাপ কার্যকর ভূমিকা পালন করে।

বিভেদাংকের প্রয়োজনীয়তা (Importance of Measures of Dispersion)

বিভেদাঙ্ক (Measures of Dispersion) একটি ডেটাসেটের মানগুলোর বৈচিত্র্য বা ছড়িয়ে পড়া সম্পর্কে ধারণা দেয়। এটি ডেটার বিশ্লেষণে গুরুত্বপূর্ণ ভূমিকা পালন করে। বিভিন্ন পরিস্থিতিতে বিভেদাংকের প্রয়োজনীয়তা নিচে আলোচনা করা হলো:

১. ডেটার বৈচিত্র্য নির্ধারণ

বিভেদাঙ্ক ডেটাসেটের মানগুলোর মধ্যে কতটা ছড়িয়ে পড়া বা পরিবর্তনশীলতা আছে তা নির্ধারণ করে। এটি বোঝায় যে ডেটাগুলো গড়ের চারপাশে কতটা ঘনিষ্ঠভাবে বা দূরত্বে ছড়ানো।
উদাহরণ:
একটি কোম্পানির কর্মচারীদের বেতন বিশ্লেষণে বিভেদাঙ্ক ব্যবহার করলে বেতনের বৈচিত্র্য সম্পর্কে ধারণা পাওয়া যায়।

২. ডেটাসেটের স্থিতিশীলতা পরিমাপ

কোনো ডেটাসেট কতটা স্থিতিশীল তা বিভেদাঙ্কের মাধ্যমে নির্ধারণ করা যায়।

• বিভেদাঙ্ক কম হলে ডেটাসেট বেশি স্থিতিশীল।
• বিভেদাঙ্ক বেশি হলে ডেটাসেট কম স্থিতিশীল।

উদাহরণ:
বিনিয়োগের ঝুঁকি পর্যালোচনার ক্ষেত্রে বিভেদাঙ্ক ব্যবহৃত হয়।

৩. ডেটাসেটের তুলনা

দুটি বা ততোধিক ডেটাসেটের বৈচিত্র্যের তুলনা করতে বিভেদাঙ্ক অপরিহার্য।
উদাহরণ:
একটি স্কুলের দুটি ক্লাসের ছাত্রদের পরীক্ষার ফলাফলের বৈচিত্র্য তুলনা করার জন্য বিভেদাঙ্ক ব্যবহার করা হয়।

৪. বৈজ্ঞানিক গবেষণা ও সিদ্ধান্ত গ্রহণ

বিভিন্ন বৈজ্ঞানিক গবেষণায় বিভেদাঙ্ক ব্যবহার করে ডেটার বৈচিত্র্য বিশ্লেষণ করা হয়, যা সঠিক সিদ্ধান্ত গ্রহণে সহায়তা করে।
উদাহরণ:
স্বাস্থ্য গবেষণায় রোগীদের রক্তচাপের মানের বৈচিত্র্য নির্ধারণে বিভেদাঙ্ক ব্যবহৃত হয়।

৫. বহিরাগত মান (Outliers) শনাক্তকরণ

বিভেদাঙ্ক ব্যবহার করে ডেটাসেটে বহিরাগত মান বা অস্বাভাবিক মান শনাক্ত করা যায়।
উদাহরণ:
একটি উৎপাদন প্রক্রিয়ায় যন্ত্রাংশের আকারের মধ্যে কোনো অস্বাভাবিক পরিবর্তন হলে বিভেদাঙ্কের সাহায্যে তা ধরা যায়।

৬. পরিসংখ্যানিক মডেল তৈরিতে সহায়তা

পরিসংখ্যানিক মডেল তৈরিতে বিভেদাঙ্ক একটি গুরুত্বপূর্ণ উপাদান। এটি ডেটার বৈচিত্র্যের উপর ভিত্তি করে মডেলের নির্ভুলতা নিশ্চিত করতে সাহায্য করে।

৭. ঝুঁকি ব্যবস্থাপনা

বিনিয়োগ এবং ঝুঁকি ব্যবস্থাপনায় বিভেদাঙ্ক ব্যবহার করা হয়। ডেটার বৈচিত্র্য বিশ্লেষণ করে ঝুঁকি কমানোর কৌশল নির্ধারণ করা যায়।

৮. গুণমান নিয়ন্ত্রণ (Quality Control)

উৎপাদন প্রক্রিয়ার গুণমান নিশ্চিত করতে বিভেদাঙ্ক ব্যবহৃত হয়।
উদাহরণ:
যদি উৎপাদিত পণ্যের বৈচিত্র্য কম থাকে, তবে পণ্যটি মানসম্পন্ন হিসেবে বিবেচিত হয়।

সারসংক্ষেপ

বিভেদাঙ্ক একটি গুরুত্বপূর্ণ পরিসংখ্যানিক মাপকাঠি যা ডেটাসেটের বৈচিত্র্য, স্থিতিশীলতা, এবং মানের প্রকৃতি বুঝতে সাহায্য করে। এটি সিদ্ধান্ত গ্রহণ, গবেষণা, এবং বিভিন্ন ক্ষেত্রের কার্যক্রম পরিচালনার জন্য অপরিহার্য। বিভেদাঙ্ক ছাড়া ডেটা বিশ্লেষণ অসম্পূর্ণ থেকে যায়।

ভেদাংক (Variance), বিভেদাংক (Dispersion), ও সহভেদাংক (Coefficient of Variation)

পরিসংখ্যানের এই তিনটি গুরুত্বপূর্ণ মাপকাঠি ডেটাসেটের বৈচিত্র্য, স্থিতিশীলতা এবং তুলনামূলক বৈশিষ্ট্য নির্ধারণে ব্যবহৃত হয়। এগুলো সম্পর্কে বিস্তারিত আলোচনা নিচে উপস্থাপন করা হলো।

ভেদাংক (Variance)

সংজ্ঞা:
ভেদাংক হলো একটি ডেটাসেটের মানগুলোর গড় থেকে কতটা বিচ্যুতি ঘটেছে তার গড় বর্গ। এটি ডেটাসেটের বৈচিত্র্য পরিমাপের জন্য একটি গুরুত্বপূর্ণ মাপকাঠি।

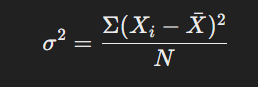
ভেদাংক নির্ণয়ের সূত্র:

যেখানে,

উদাহরণ:

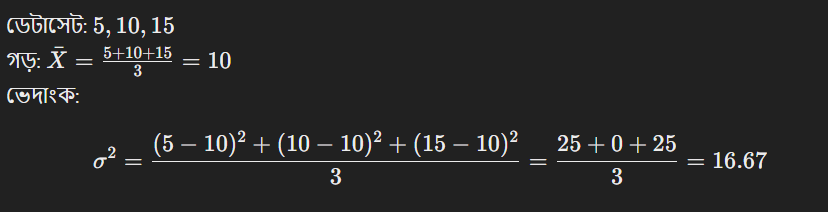
বৈশিষ্ট্য:

• এটি ডেটাসেটের বৈচিত্র্যের একটি নির্ভুল পরিমাপ।
• বর্গমূলের মাধ্যমে মান বিচ্যুতি (Standard Deviation) নির্ণয় করা যায়।

বিভেদাংক (Dispersion)

সংজ্ঞা:
বিভেদাংক হলো ডেটাসেটের মানগুলোর ছড়িয়ে পড়া বা বৈচিত্র্যের পরিমাপ। এটি ডেটার সর্বোচ্চ ও সর্বনিম্ন মানের মধ্যকার পার্থক্য, গড় থেকে বিচ্যুতি, বা অন্যান্য সূচকের মাধ্যমে নির্ধারণ করা হয়।

প্রকারভেদ:
১. বিস্তার (Range): সর্বোচ্চ এবং সর্বনিম্ন মানের পার্থক্য।
Range = Maximum Value - Minimum Value

২. আন্তঃচতুর্ভাগ বিস্তার (Interquartile Range - IQR):
IQR= Q3 - Q1

৩. গড় বিচ্যুতি (Mean Deviation):

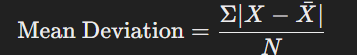
৪. মান বিচ্যুতি (Standard Deviation):

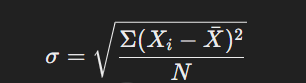
গুরুত্ব:

• ডেটাসেটের বৈচিত্র্য এবং স্থিতিশীলতা নির্ধারণে বিভেদাংক গুরুত্বপূর্ণ ভূমিকা পালন করে।
• এটি বহিরাগত মান বা অস্বাভাবিক বৈচিত্র্য সনাক্তে সহায়তা করে।

সহভেদাংক (Coefficient of Variation - CV)

সংজ্ঞা:
সহভেদাংক হলো ডেটাসেটের মান বিচ্যুতি এবং গড়ের অনুপাত, যা শতাংশে প্রকাশ করা হয়। এটি বিভিন্ন ডেটাসেটের তুলনা করার জন্য ব্যবহৃত হয়।

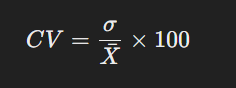
সহভেদাংক নির্ণয়ের সূত্র:

যেখানে,

উদাহরণ:

গুরুত্ব:

• সহভেদাংক ডেটাসেটের আপেক্ষিক বৈচিত্র্য প্রকাশ করে।
• এটি ভিন্ন একক বিশিষ্ট ডেটাসেটের তুলনার জন্য কার্যকর।

তুলনামূলক আলোচনা

সারসংক্ষেপ

• ভেদাংক ডেটাসেটের মানগুলোর গড় থেকে বিচ্যুতি নির্ধারণে কার্যকর।
• বিভেদাংক ডেটাসেটের বৈচিত্র্য সম্পর্কে সামগ্রিক ধারণা দেয়।
• সহভেদাংক বিভিন্ন ডেটাসেটের আপেক্ষিক বৈচিত্র্য তুলনা করতে ব্যবহৃত হয়।

এই তিনটি মাপকাঠি ডেটা বিশ্লেষণে ভিন্ন ভিন্ন প্রয়োজনে ব্যবহৃত হয় এবং প্রতিটির নিজস্ব গুরুত্ব রয়েছে।